Nombre:
Blanca Flor Martinez Martinez
Modulo:
Análisis Integral De Funciones
Grupo:
6206 Informatica
TEMARIO
UNIDAD 2
*Determinación de la integridad indefinida
1.1.Calculo e derivadas mediante formulas inmediatas de integración.
Objetivo 1.1.1
Resuelve ejercicios de anti derivadas inmediata considerando lo siguiente:
*Formulación
*Procedimientos
*Resultados
A) Determinación de diferenciales
*Interpretación gráfica de la diferencial de la variable dependiente.
*Definición de la variable independiente y dependiente.
*Reglas de la diferenciación.
B) Calculo de anti derivadas
*¨Definición.
*Regla de anti derivadas para potencias.
*Formulas e integrantes inmediatas.
-Algebraicas
-Logarítmicas
-Exponenciales
-Trigonométricas
*Solución de problemas.
Objetivo 1.2
Resuelve integrales indefinidas mediante métodos de integración.
Objetivo 1.2.1
Resuelve ejercicios y aplicaciones de la integral indefinida de acuerdo con lo siguiente:
*Ejercicios con el método de:
-Cambio de variable.
-Por partes.
-Fracciones parciales.
-Solución de tablas.
*Problemas de algún contexto de:
-Ingeniera
- Ciencias
-Economía
-Administración
A) Solución por cambio de variable o sustitución .
-Algebraicas.
-Trigonométricas.
-Exponenciales.
-Logarítmicas.
B) Soluciones por partes
*Casos
*Aplicas ion
*Formula
C)Solución por fracciones parciales.
*¨Casos
*Aplicación
D) Solución por sustitución trigonométrica.
*Casos
*Aplicación
E) Solución por tablas.
*Trigonométricas
*Logarítmicas
*Algebraicas
*Exponenciales
*Irracionales
F)Calculo de ecuación diferencial.
*De variables separables
*Resolución de problemas aplicados en diferentes contextos.
*Ciencias e ingeniería
*Economía y administración
UNIDAD 2
Determinación de la integral definida
Objetivo 2.1
Calculo de integrales definidas mediante formulas directas y métodos.
Objetivo 2.1.1
Resuelve ejercicios de la integral definida considerando lo siguiente:
*Formulas
*Métodos
*Procedimientos
*Resultados
A) Determinación de la integral definida.
*Notación de sumatoria
*Concepto de integral definida en un intervalo
B) Aplicación del teorema fundamental del calculo
*Definición
*Formulas directas
*Calculo de integrales definidas por métodos
-Por cambio e variable
-Por partes
-Por fracciones parciales
Objetivo 2.2
Calculo de áreas mediante integrales definidas
Objetivo 2.2.1
Resuelve aplicaciones de la integral definida de acuerdo a lo siguiente
*Ejercicios de calculo de áreas
*Con una función
*Con dos funciones
*Con tres funciones
*Problemas de algún contexto de:
-Ciencias
-Ingeniera
-Economía
-Administración
A)Calculo de áreas de figuras planas.
*Con una función
*Sobre el eje x
*Bajo el eje x
*Entre el eje x
*Con dos y tres funciones
*Sobre y debajo del eje x
*Entre el eje x
*Por la derecha del eje x
*Entre el eje x
*Entre dos gráficas
*Entre tres gráficas
B)Resolución de problemas aplicadas en diferentes contextos
*Ciencias
*Ingeniería
*Economía
*Administración
DETERMINACIÓN DE LA INTEGRIDAD INDEFINIDA
Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
Propiedades de la integral indefinida1. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.
∫ k f(x) dx = k ∫f(x) dx
Propiedades de la integral indefinida1. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.
∫ k f(x) dx = k ∫f(x) dx

En la siguiente imagen se muestran las formulas de las integrales
DETERMINACIÓN DE DIFERENCIALES
Determinación de diferenciales.
Interpretación gráfica de la diferencial de la variable dependiente.
Una variable dependiente es aquella cuyos valores dependen de los que tomen otra variable.
La variable dependiente en una función se suele representar por y.
La variable dependiente se representa en el eje ordenadas.
La variable y está en función de la variable x, que es la variable independiente.
Ejemplos
El precio que pagamos por las patatas depende del número de kilogramos que compremos.
x = Kg de patatas 1 2 3 4 5
y = Precio en € 2 4 6 8 10
El precio de un viaje en taxi viene dado por:
y = 3 + 0.5 x
Siendo x el tiempo en minutos que dura el viaje.
x 10 20 30
y= 3 + 0.5x 8 13 18
Reglas de diferenciación.
Función de una variable-de forma
!
Y = f (x) donde f significa cualquier función. En
Economía, generalmente, suponemos que las funciones son continuamente
Diferenciables. k es un constante.
1. Regla de la función constante
Determinación de diferenciales.
Interpretación grafica de la diferencial de la variable dependiente.
Una variable dependiente es aquella cuyos valores dependen de los que tomen otra variable.
La variable dependiente en una función se suele representar por y.
La variable dependiente se representa en el eje ordenadas.
La variable y está en función de la variable x, que es la variable independiente.
Ejemplos
El precio que pagamos por las patatas depende del número de kilogramos que compremos.
x = Kg de patatas 1 2 3 4 5
y = Precio en € 2 4 6 8 10
El precio de un viaje en taxi viene dado por:
y = 3 + 0.5 x
Siendo x el tiempo en minutos que dura el viaje.
x 10 20 30
y= 3 + 0.5x 8 13 18
Reglas de diferenciación.
Función de una variable-de forma
!
Y = f (x) donde f significa cualquier función. En
Economía, generalmente, suponemos que las funciones son continuamente
Diferenciales. que es un constante.
IDENTIFICACIÓN GRÁFICA DE LA DIFERENCIAL DE LA VARIABLE INDEPENDIENTE
Una distinción de particular importancia es aquella entre variables dependientes e independientes. Los términos“dependiente” e “independiente” se utilizan para representar una relación de “causalidad” entre dos variables. La relación es la siguiente: el valor de la variable dependiente ‘depende’ del valor de la variable independiente. En otras palabras: la variable independiente determina, en alguna medida (medida que puede ser mayor o menor), el valor de la variable dependiente. Utilizando otros términos, la variable independiente “causa” la variable dependiente. O sea que el comportamiento de la variable dependiente se podría predecir sobre la base del comportamiento de la variable independiente.
Por ejemplo, consideremos la siguiente hipótesis: un buen maestro causa que los estudiantes aprendan. En este caso, “buen maestro” es la variable independiente, mientras que “grado de aprendizaje” (de los estudiantes) es la variable dependiente. Pero no siempre es fácil, o ni siquiera posible, saber cuál es la variable dependiente y cuál la independiente en una relación. Siguiendo con el ejemplo anterior, ¿es cierto que el aprendizaje de los niños resulta de la calidad del maestro? Por ejemplo, ¿el hecho de que los estudiantes de la escuela A tengan un mejor rendimiento que los de la escuela B significa que los maestros de la escuela A son mejores que los de la escuela B? Para empezar, quizás los estudiantes de la escuela A son más aventajados en cierto respecto, o hay otros elementos que causan ese mayor aprendizaje que no tienen nada que ver con los maestros.
El problema de la determinación de causalidad (¿cuáles variables son dependientes y cuáles independientes?) es uno de los problemas más serios que enfrenta la estadística. El análisis empírico o estadístico sólo puede decirnos si dos variables parecen estar relacionadas, pero no puede decirnos: (a) si de hecho existe una relación de dependencia y (b) cuál es la dirección de dicha relación (cuál es la “causa” y cuál el efecto o la variable “causada”). Necesitamos una “teoría” para dar plausibilidad a una relación empírica.
Considere la siguiente cuestión: ¿Es el aumento del ingreso per capita de un país que causa mejoras en el nivel de educación o la mejora en el nivel de educación que causa mejoras en el ingreso per capita? ¿O tal vez un tercer factor es la causa de ambos? ¿Cultura? Este complejo y viejo debate no se puede resolver sólo sobre la base del análisis estadístico, aunque la estadística es un importante instrumento en nuestros continuos esfuerzos por dilucidar estas cuestiones. El debate mencionado ha persistido por décadas, además, porque muchas de las teorías que han sido propuestas para explicar la relación entre educación y desarrollo económico no pueden ser refutadas sólo sobre la base del análisis empírico.
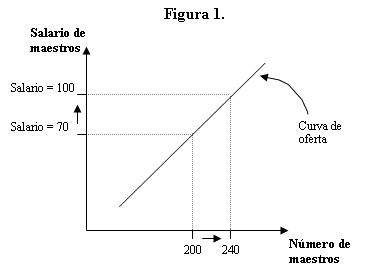
Vayamos por un momento al tema de la interpretación de gráficos (tratado en mayor detalle en los módulos 3 y 4 de esta guía). Un gráfico representa una relación entre por lo menos dos variables. En matemáticas y geometría, la variable dependiente se denomina X y se representa en el eje horizontal del gráfico, mientras que la variable independiente se llama Y (o ‘independiente’, para facilitar la memorización) y se representa en el eje vertical. En la Figura 1, a continuación, se muestra un ejemplo de una “curva de oferta” que presenta la relación entre dos variables: el salario de los maestros y la cantidad o número de maestros disponibles o que ofrecen sus servicios.
En el gráfico siguiente, ¿puede usted identificar cuál es la variable dependiente y cuál la independiente?
Por ejemplo, consideremos la siguiente hipótesis: un buen maestro causa que los estudiantes aprendan. En este caso, “buen maestro” es la variable independiente, mientras que “grado de aprendizaje” (de los estudiantes) es la variable dependiente. Pero no siempre es fácil, o ni siquiera posible, saber cuál es la variable dependiente y cuál la independiente en una relación. Siguiendo con el ejemplo anterior, ¿es cierto que el aprendizaje de los niños resulta de la calidad del maestro? Por ejemplo, ¿el hecho de que los estudiantes de la escuela A tengan un mejor rendimiento que los de la escuela B significa que los maestros de la escuela A son mejores que los de la escuela B? Para empezar, quizás los estudiantes de la escuela A son más aventajados en cierto respecto, o hay otros elementos que causan ese mayor aprendizaje que no tienen nada que ver con los maestros.
El problema de la determinación de causalidad (¿cuáles variables son dependientes y cuáles independientes?) es uno de los problemas más serios que enfrenta la estadística. El análisis empírico o estadístico sólo puede decirnos si dos variables parecen estar relacionadas, pero no puede decirnos: (a) si de hecho existe una relación de dependencia y (b) cuál es la dirección de dicha relación (cuál es la “causa” y cuál el efecto o la variable “causada”). Necesitamos una “teoría” para dar plausibilidad a una relación empírica.
Considere la siguiente cuestión: ¿Es el aumento del ingreso per capita de un país que causa mejoras en el nivel de educación o la mejora en el nivel de educación que causa mejoras en el ingreso per capita? ¿O tal vez un tercer factor es la causa de ambos? ¿Cultura? Este complejo y viejo debate no se puede resolver sólo sobre la base del análisis estadístico, aunque la estadística es un importante instrumento en nuestros continuos esfuerzos por dilucidar estas cuestiones. El debate mencionado ha persistido por décadas, además, porque muchas de las teorías que han sido propuestas para explicar la relación entre educación y desarrollo económico no pueden ser refutadas sólo sobre la base del análisis empírico.
Vayamos por un momento al tema de la interpretación de gráficos (tratado en mayor detalle en los módulos 3 y 4 de esta guía). Un gráfico representa una relación entre por lo menos dos variables. En matemáticas y geometría, la variable dependiente se denomina X y se representa en el eje horizontal del gráfico, mientras que la variable independiente se llama Y (o ‘independiente’, para facilitar la memorización) y se representa en el eje vertical. En la Figura 1, a continuación, se muestra un ejemplo de una “curva de oferta” que presenta la relación entre dos variables: el salario de los maestros y la cantidad o número de maestros disponibles o que ofrecen sus servicios.
En el gráfico siguiente, ¿puede usted identificar cuál es la variable dependiente y cuál la independiente?

(El siguiente módulo trata el tema de cómo leer gráficos. Si tuvo problemas en la interpretación de la Figura 1, el módulo siguiente le debería ayudar a interpretarla con mayor confianza.)
DEFINICIÓN DE LA VARIABLE DEPENDIENTE
Una variable dependiente es aquella cuyos valores dependen de los que tomen otra variable.
La variable dependiente en una función se suele representar por y.
La variable dependiente se representa en el eje ordenadas.
La variable y está en función de la variable x, que es la variable independiente.
Ejemplos
El precio que pagamos por las patatas depende del número de kilogramos que compremos.
| x = Kg de patatas | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| y = Precio en € | 2 | 4 | 6 | 8 | 10 |
VARIABLE INDEPENDIENTE
Una variable independiente es aquella cuyo valor no depende del de otra variable.
La variable independiente en una función se suele representar por x.
La variable independiente se representa en el eje de abscisas.
La variable y, llamada variable dependiente, está en función de la variable x, que es la variable independiente.
Ejemplos
El precio que pagamos por las patatas depende del número de kilogramos que compremos.
| x = Kg de patatas | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| y = Precio en € | 2 | 4 | 6 | 8 | 10 |
REGLAS DE LA DIFERENCIACIÓN
1. Regla de la función constante
!
y = f(x) = k
!
dy
dx = dk
dx =0
2. Regla de la función potencial
!
y = f(x) = kxn
!
dy
dx = f "(x) = knxn#1
• Ejemplo 1
!
y = 7x3 " dy
dx =(7#3)x3$1 =21x2
• Ejemplo 2
!
y = 7x
1
4 " dy
dx = 7#
1
4
$
%
& '
(
) x
1
4
*1
= 7
4
x
*3
4
3. Regla de la función logaritmo natural (base de ‘e’).
!
y =lnx " dy
dx = 1
x
La versión general
!
y =ln f(x)" dy
dx = f #(x)
f(x)
4. Regla de la función exponencial
!
y =ex " dy
dx =ex
La versión general
!
y =ef(x) " dy
dx = f #(x)ef(x)
Dos o más funciones de la misma variable-
!
f(x),g(x),h(x) son funciones.
1. Regla de la suma
!
y = f(x)± g(x)
!
d[f(x)± g(x)]
dx = df(x)
dx
±
dg(x)
dx = f "(x)± g"(x)
• Ejemplo 1
!
y = 7x4 +2x3 "3x + 37# dy
dx =28x3 +6x2 "3
• Ejemplo 2
!
y = ax2 +bx +c " dy
dx =2ax +b
• Ejemplo 3
!
y = ax" +bx# +c $ dy
dx ="ax"%1 +#bx#%1
2. Regla del producto
!
y = f(x)g(x)
!
d[f(x)g(x)]
dx = f(x)
dg(x)
dx
+ g(x)
df(x)
dx = f(x)g"(x)+ g(x)f "(x)
• Ejemplo 1
!
y =(2x + 3) 3x2
( ) " dy
dx =(2x + 3)(6x)+(2) 3x2
( ) =18x2 +18x o, en
este caso podemos multiplicar primer, y después tomamos la derivada.
!
y =(2x + 3) 3x2
( ) =6x3 +9x2 " dy
dx =18x2 +18x. Pero, en algunos casos no se
puede.
2
• La regla sirve en los casos de más que 2 funciones. Si
!
y = f(x)g(x)h(x)
!
d[f(x)g(x)h(x)]
dx = f(x)h(x)
dg(x)
dx
+ g(x)h(x)
df(x)
dx
+ g(x)f(x)
dh(x)
dx =
f(x)h(x)g"(x)+ g(x)h(x)f "(x)+ g(x)f(x)h"(x)
3. Regla de cociente
!
y = f(x)
g(x) " dy
dx = g(x)f #(x)$ f(x)g#(x)
[g(x)]
2
• Ejemplo 1
!
y = (2x "3)
(x +1) # dy
dx = (x +1)2"(2x "3)1
(x +1)
2 = 5
(x +1)
2
• Ejemplo 2
!
y = ax2
( +b)
cx
" dy
dx = cx2ax # ax2
( +b)c
(cx)
2 = c ax2
( #b)
c2
x2 = ax2 #b
cx2
Funciones de variables diferentes-
!
x,y,w,z son variables y
!
f(y),g(x),h(w) son
funciones.
1. Regla de la cadena
!
z = f(y) y = g(x)"
dz
dx = dz
dy
dy
dx = f #(y)g#(x) También
podemos obtener este resultado con la sustitución de
!
g(x) en la función
!
z = f(y) = f[g(x)] "
dz
dx = f #[g(x)]g#(x) = f #(y)g#(x)
• Ejemplo 1
!
z = 3y2 y =2x +5"
dz
dx =(6y)(2) =12y =12(2x +5) =24x +60
• Ejemplo 2
!
z = x2
( + 3x "2)
17
Sea que
!
y = x2
( + 3x "2) # z = y17 Entonces
!
dz
dy =17y16 dy
dx =2x + 3
!
dz
dx = dz
dy
dy
dx = 17y16 ( )(2x + 3) =17 x2
( + 3x "2)
16(2x + 3)
Usos en economía (funciones de una variable).
• Función de producción donde hay nada más un factor de producción, digamos el
trabajo.
!
y = f(l)" dy
dl = f #(l) la derivada es el producto marginal de trabajo
• Función de consumo en el modelo keynesiano tradicional. Consumo actual es
una función de ingreso actual (la única variable) y una cantidad fija, se
denomina consumo autónomo.
!
C=C +c(Y)"
dC
dY =c#(Y) La derivada es la
propensión marginal de consumo. Típicamente, en los cursos introductorias de
macro, la función
!
c(Y) es lineal (c es constante) tanto que
!
c(Y) =cY "
dC
dY =c. 3
• Elasticidades en un punto-Sea que la demanda de mercado tiene una forma
!
Qd =Q(P), P es el precio del producto.
!
dQd
dP =Q"(P) La elasticidad de
demanda respecto el precio (del mismo bien) es
!
"
d = dQd
dP
P
Qd
• Tasas de crecimiento. Una variable y cambio con tiempo t. Escribimos
!
y = f(t)" dy
dt = f #(t) La tasa de cambio (o crecimiento) de y es
!
dy
dt
y = f "(t)
f(t)
.
Obsérvense que podemos escribir la función
!
y = f(t) en logaritmos
!
lny =ln f(t) y usamos la regla de logaritmos para obtener la tasa de
crecimiento.
!
dlny
dt = f "(t)
f(t) =
dy
d
REGLAS DE ANTI DERIVADAS PARA POTENCIAS
1. Regla de la función constante
!
y = f(x) = k
!
dy
dx = dk
dx =0
2. Regla de la función potencial
!
y = f(x) = kxn
!
dy
dx = f "(x) = knxn#1
• Ejemplo 1
!
y = 7x3 " dy
dx =(7#3)x3$1 =21x2
• Ejemplo 2
!
y = 7x
1
4 " dy
dx = 7#
1
4
$
%
& '
(
) x
1
4
*1
= 7
4
x
*3
4
3. Regla de la función logaritmo natural (base de ‘e’).
!
y =lnx " dy
dx = 1
x
La versión general
!
y =ln f(x)" dy
dx = f #(x)
f(x)
4. Regla de la función exponencial
!
y =ex " dy
dx =ex
La versión general
!
y =ef(x) " dy
dx = f #(x)ef(x)
Dos o más funciones de la misma variable-
!
f(x),g(x),h(x) son funciones.
1. Regla de la suma
!
y = f(x)± g(x)
!
d[f(x)± g(x)]
dx = df(x)
dx
±
dg(x)
dx = f "(x)± g"(x)
• Ejemplo 1
!
y = 7x4 +2x3 "3x + 37# dy
dx =28x3 +6x2 "3
• Ejemplo 2
!
y = ax2 +bx +c " dy
dx =2ax +b
• Ejemplo 3
!
y = ax" +bx# +c $ dy
dx ="ax"%1 +#bx#%1
2. Regla del producto
!
y = f(x)g(x)
!
d[f(x)g(x)]
dx = f(x)
dg(x)
dx
+ g(x)
df(x)
dx = f(x)g"(x)+ g(x)f "(x)
• Ejemplo 1
!
y =(2x + 3) 3x2
( ) " dy
dx =(2x + 3)(6x)+(2) 3x2
( ) =18x2 +18x o, en
este caso podemos multiplicar primer, y después tomamos la derivada.
!
y =(2x + 3) 3x2
( ) =6x3 +9x2 " dy
dx =18x2 +18x. Pero, en algunos casos no se
puede.
2
• La regla sirve en los casos de más que 2 funciones. Si
!
y = f(x)g(x)h(x)
!
d[f(x)g(x)h(x)]
dx = f(x)h(x)
dg(x)
dx
+ g(x)h(x)
df(x)
dx
+ g(x)f(x)
dh(x)
dx =
f(x)h(x)g"(x)+ g(x)h(x)f "(x)+ g(x)f(x)h"(x)
3. Regla de cociente
!
y = f(x)
g(x) " dy
dx = g(x)f #(x)$ f(x)g#(x)
[g(x)]
2
• Ejemplo 1
!
y = (2x "3)
(x +1) # dy
dx = (x +1)2"(2x "3)1
(x +1)
2 = 5
(x +1)
2
• Ejemplo 2
!
y = ax2
( +b)
cx
" dy
dx = cx2ax # ax2
( +b)c
(cx)
2 = c ax2
( #b)
c2
x2 = ax2 #b
cx2
Funciones de variables diferentes-
!
x,y,w,z son variables y
!
f(y),g(x),h(w) son
funciones.
1. Regla de la cadena
!
z = f(y) y = g(x)"
dz
dx = dz
dy
dy
dx = f #(y)g#(x) También
podemos obtener este resultado con la sustitución de
!
g(x) en la función
!
z = f(y) = f[g(x)] "
dz
dx = f #[g(x)]g#(x) = f #(y)g#(x)
• Ejemplo 1
!
z = 3y2 y =2x +5"
dz
dx =(6y)(2) =12y =12(2x +5) =24x +60
• Ejemplo 2
!
z = x2
( + 3x "2)
17
Sea que
!
y = x2
( + 3x "2) # z = y17 Entonces
!
dz
dy =17y16 dy
dx =2x + 3
!
dz
dx = dz
dy
dy
dx = 17y16 ( )(2x + 3) =17 x2
( + 3x "2)
16(2x + 3)
Usos en economía (funciones de una variable).
• Función de producción donde hay nada más un factor de producción, digamos el
trabajo.
!
y = f(l)" dy
dl = f #(l) la derivada es el producto marginal de trabajo
• Función de consumo en el modelo keynesiano tradicional. Consumo actual es
una función de ingreso actual (la única variable) y una cantidad fija, se
denomina consumo autónomo.
!
C=C +c(Y)"
dC
dY =c#(Y) La derivada es la
propensión marginal de consumo. Típicamente, en los cursos introductorias de
macro, la función
!
c(Y) es lineal (c es constante) tanto que
!
c(Y) =cY "
dC
dY =c. 3
• Elasticidades en un punto-Sea que la demanda de mercado tiene una forma
!
Qd =Q(P), P es el precio del producto.
!
dQd
dP =Q"(P) La elasticidad de
demanda respecto el precio (del mismo bien) es
!
"
d = dQd
dP
P
Qd
• Tasas de crecimiento. Una variable y cambio con tiempo t. Escribimos
!
y = f(t)" dy
dt = f #(t) La tasa de cambio (o crecimiento) de y es
!
dy
dt
y = f "(t)
f(t)
.
Obsérvense que podemos escribir la función
!
y = f(t) en logaritmos
!
lny =ln f(t) y usamos la regla de logaritmos para obtener la tasa de
crecimiento.
!
dlny
dt = f "(t)
f(t) =
dy
d
FORMULAS E INTEGRALES INMEDIATAS
*ALGEBRAICAS *LOGARÍTMICAS *EXPONENCIALES *TRIGONOMÉTRICAS
Integrales inmediatas
Integrales reducibles a inmediatas de tipo potencial:
Siempre que en el integrando aparezca una función elevada a una constante, si lo que la multiplica es al menos en su parte variable la derivada de la función, se podrá ajustar con constantes y será una integral inmediata de tipo potencial.
Ejemplo:

Integrales reducibles a inmediatas de tipo exponencial.
Siempre que en el integrando aparezca una función, si lo que la multiplica es al menos en su parte variable la derivada de la función, se podrá ajustar con constantes, y será una inmediata de tipo exponencial.
Ejemplo:
Integrales reducible a inmediatas de tipo logarítmico.
Si en el integrando aparece un cociente, si el numerador es al menos en su parte variable la derivada del denominador, se podrá ajustar con constantes, y será una integral inmediata de tipo logarítmico.
Ejemplo:
Integrales reducibles a inmediatas de tipo trigonométricas inversas.
Si en el integrando aparece una expresión de alguno de los tipos:

O incluso sin raíz en el denominador. Podemos aplicar el método de los 4 pasos que consiste en:
Paso 1:: Se multiplican numerador y denominador por la raíz cuadrada de cuatro veces el valor absoluto del coeficiente numérico del término en x2.
Paso 2: :Se expresa el término interior a la raíz obtenido anteriormente en la forma
Paso 3:: Se divide numerador y denominador por la raíz cuadrada de p.
Paso 4:: Se ajusta por constantes el resultado obtenido a alguna de las integrales inmediatas de tipo inversa de las trigonométricas.
Ejemplo:
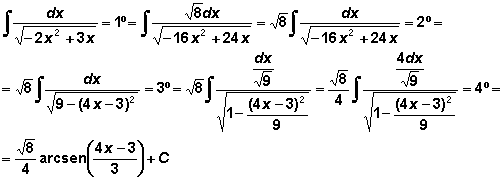 |
SOLUCIÓN DE PROBLEMAS
Diariamente es necesario enfrentar problemas y conflictos a los cuales se les deben encontrar soluciones aceptables de acuerdo al contexto. El proceso de solucionar problemas implica una serie de capacidades y habilidades del pensamiento que es importante desarrollar y evaluar en la preparación académica.
La resolución de problemas es una actividad cognitiva que consiste en proporcionar una respuesta-producto a partir de un objeto o de una situación.
RESUELVE EJERCICIOS Y APLICACIONES DE LA INTEGRAL INDEFINIDA DE ACUERDO A LO SIGUIENTE
*CAMBIO DE VARIABLE
1º Se hace el cambio de variable y se diferencia en los dos términos:
Se despeja u y dx, sutituyendo en la integral:

2º Si la integral resultante es más sencilla, integramos:
3º Se vuelve a la variable inicial:
CALCULO DE ECUACIÓN DIFERENCIAL
Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o más funciones desconocidas. Dependiendo del número de variables independientes respecto de las que se deriva, las ecuaciones diferenciales se dividen en:
- Ecuaciones diferenciales ordinarias: aquellas que contienen derivadas respecto a una sola variable independiente.
- Ecuaciones en derivadas parciales: aquellas que contienen derivadas respecto a dos o más variables.
*DE VARIABLES SEPARABLES
Se dice que una ecuación diferencial se puede separar si es posible escibir la ecuación en la forma
El factor integrante  , es decir, si multiplicamos esta expresión por esta cantidad tendremos
, es decir, si multiplicamos esta expresión por esta cantidad tendremos
lo cual resulta fácil de integrar siendo  una función de la variable x y
una función de la variable x y  una función de y, sin embargo, para la obtención de la solución es importante considerar si las funciones son integrables.
una función de y, sin embargo, para la obtención de la solución es importante considerar si las funciones son integrables.
Ejemplo de variables separables
1.- Encontremos la solución de la ecuación diferencial
Solución:
despejando tenemos:
integrando

despejando
DETERMINACIÓN DE LA INTEGRAL DEFINIDA
Cuando estudiamos el problema del área y el problema de la distancia analizamos que tanto el valor del área debajo de la gráfica de una función como la distancia recorrida por un objeto se puede calcular aproximadamente por medio de sumas o bien exactamente como el límite de una suma.
(se utiliza el valor de la función en el extremo izquierdo de cada subintervalo)
(se utiliza el valor de la función en el extremo derecho de cada subintervalo)
(se utiliza el valor de la función en cualquier punto de cada subintervalo)
Este tipo de límites aparece en una gran variedad de situaciones incluso cuando f no es necesariamente una función positiva. Teniendo en cuenta lo expresado surge la necesidad de dar un nombre y una notación a este tipo de límites.
Definición 1: Si f es una función continua sobre el intervalo [a, b], entonces la integral definida de f de a a b, que se indica 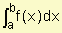 es el número:
es el número:
(la función se evalúa en el extremo izquierdo de cada subintervalo [xi-1, xi] con i = 1, .., n)
Definición 2: Si f es una función continua sobre el intervalo [a, b], entonces la integral definida de f de a a b, que se indica  es el número:
es el número:
(la función se evalúa en el extremo derecho de cada subintervalo [xi-1, xi] con i = 1, .., n)
Definición 3: Si f es una función continua sobre el intervalo [a, b], entonces la integral definida de f de a a b, que se indica 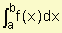 es el número:
es el número:
(la función se evalúa en cualquier punto ti de cada subintervalo [xi-1, xi] con i = 1, .., n)
El número a es el límite inferior de integración y el número b es el límite superior de integración .
Notación y terminología:
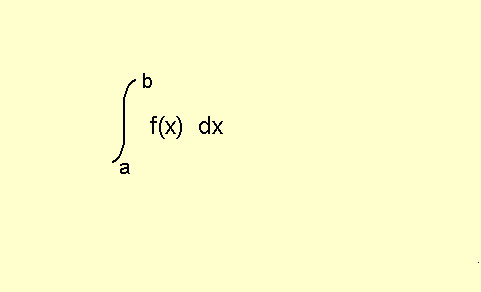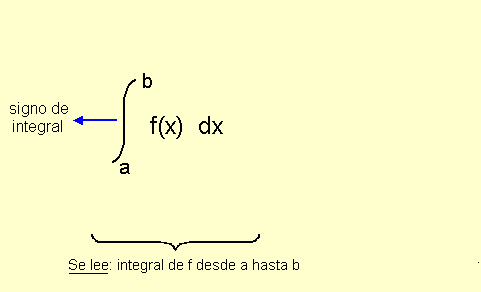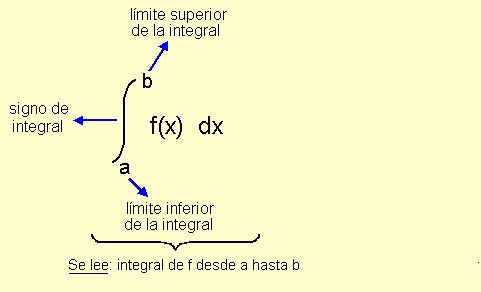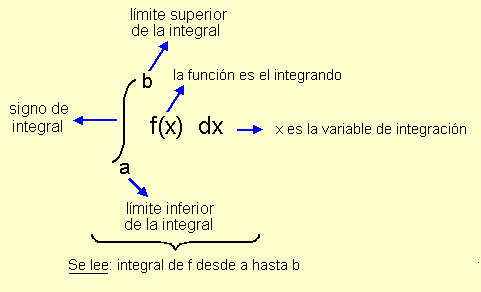
Cuando se calcula el valor de la integral definida se dice que se e valúa la integral.
La continuidad asegura que los límites en las tres definiciones existen y dan el mismo valor por eso podemos asegurar que el valor de 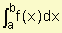 es el mismo independientemente de cómo elijamos los valores de x para evaluar la función (extremo derecho, extremo izquierdo o cualquier punto en cada subintervalo). Enunciamos entonces una definición más general.
es el mismo independientemente de cómo elijamos los valores de x para evaluar la función (extremo derecho, extremo izquierdo o cualquier punto en cada subintervalo). Enunciamos entonces una definición más general.
Definición de integral definida: Sea f una función continua definida para a £ x £ b. Dividimos el intervalo [a, b] en n subintervalos de igual ancho D x = 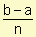 . Sean x0 = a y xn = b y además x0, x1, ...., xn los puntos extremos de cada subintervalo. Elegimos un punto ti en estos subintervalos de modo tal que ti se encuentra en el i-ésimo subintervalo [xi-1, xi] con i = 1, .., n.
. Sean x0 = a y xn = b y además x0, x1, ...., xn los puntos extremos de cada subintervalo. Elegimos un punto ti en estos subintervalos de modo tal que ti se encuentra en el i-ésimo subintervalo [xi-1, xi] con i = 1, .., n.
Entonces la integral definida de f de a a b es el número 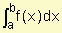 =
=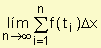 .
.
La integral definida es un número que no depende de x. Se puede utilizar cualquier letra en lugar de x sin que cambie el valor de la integral.
Aunque esta definición básicamente tiene su motivación en el problema de cálculo de áreas, se aplica para muchas otras situaciones. La definición de la integral definida es válida aún cuando f(x) tome valores negativos (es decir cuando la gráfica se encuentre debajo del eje x). Sin embargo, en este caso el número resultante no es el área entre la gráfica y el eje x.
Observación: La suma  que aparece en la definición de integral definida se llama suma de Riemann en honor al matemático alemán Bernahrd Riemann. Su definición incluía además subintervalos de distinta longitud.
que aparece en la definición de integral definida se llama suma de Riemann en honor al matemático alemán Bernahrd Riemann. Su definición incluía además subintervalos de distinta longitud.
 que aparece en la definición de integral definida se llama suma de Riemann en honor al matemático alemán Bernahrd Riemann. Su definición incluía además subintervalos de distinta longitud.
que aparece en la definición de integral definida se llama suma de Riemann en honor al matemático alemán Bernahrd Riemann. Su definición incluía además subintervalos de distinta longitud.
Definición de las sumas de Riemann: Sea f una función definida en el intervalo cerrado [a, b] y sea una división (partición) arbitraria de dicho intervalo a = x0 £ x1 £ x2 £ x3 £ ......... £ xn-1 £ xn = b donde D xi indica la amplitud o longitud del i-ésimo subintervalo. Si ti es cualquier punto del i-ésimo subintervalo la suma 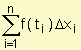 , xi-1 £ ti £ xi se llama suma de Riemann de f asociada a la partición .
, xi-1 £ ti £ xi se llama suma de Riemann de f asociada a la partición .
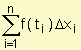 , xi-1 £ ti £ xi se llama suma de Riemann de f asociada a la partición .
, xi-1 £ ti £ xi se llama suma de Riemann de f asociada a la partición .
Si bien la integral definida había sido definida y usada con mucha anterioridad a la época de Riemann él generalizó el concepto para poder incluir una clase de funciones más amplia. En la definición de una suma de Riemann, la única restricción sobre la función f es que esté definida en el intervalo [a, b]. (antes suponíamos que f era no negativa debido a que estábamos tratando con el área bajo una curva).
Una página interesante para ampliar sobre las sumas de Riemann y visualizar animaciones resultahttp://www.dma.fi.upm.es/docencia/primerciclo/calculo/tutoriales/integracion/
Ejemplo: Halle 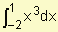
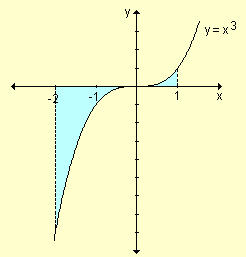
Como f(x) = x3 es continua en el intervalo [-2, 1] sabemos que es integrable.
Dividimos el intervalo en n subintervalos de igual longitud  y para el cálculo de la integral consideramos el extremo derecho de cada subintervalo ti =
y para el cálculo de la integral consideramos el extremo derecho de cada subintervalo ti = 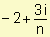 .
.
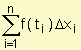 =
= 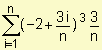 =
= 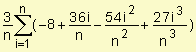
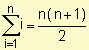
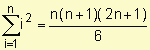
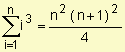
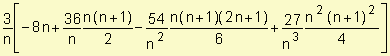
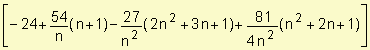
NOTACIÓN SUMATORIA RIEMANN
En matemáticas, la suma de Riemann es un método de integración numérica que nos sirve para calcular el valor de una integral definida, es decir, el área bajo una curva, este método es muy útil cuando no es posible utilizar el Teorema fundamental del cálculo. Estas sumas toman su nombre del matemático alemán Bernhard Riemann.
La suma de Riemann consiste en trazar un número finito de rectángulos dentro de un área irregular, calcular el área de cada uno de ellos y sumarlos. El problema de este método de integración numérica es que al sumar las áreas se obtiene un margen de error muy grande.
Consideremos lo siguiente:
- una función
![f:[D]\rightarrow\mathbb{R}](http://upload.wikimedia.org/math/2/9/3/293bb52f0a89d73cc4f24b6308e7471c.png)
- donde D es un subconjunto de los números reales

- una función
- I = [a, b] un intervalo cerrado contenido en D.
- Un conjunto finito de puntos {x0, x1, x2, ... xn} tales que a = x0 <x1 < x2 ... < xn = b
- crean una partición de I
- P = {[x0, x1), [x1, x2), ... [xn-1, xn]}
Si P es una partición con n elementos de I, entonces la suma de Riemann de f sobre I con la partición P se define como

- donde xi-1 ≤ yi ≤ xi. La elección de yi en este intervalo es arbitraria.
- Si yi = xi-1 para todo i, entonces denominamos S como la suma de Riemann por la izquierda.
- Si yi = xi, entonces denominamos S como la suma de Riemann por la derecha.
ÁREAS DE FIGURAS PLANAS En esta página podremos ver, si pulsamos en los iconos correspondientes que tenemos arriba, las áreas de las figuras planas siguientes:- Triángulo
- Cuadrado
- Rectángulo
- Rombo
- Trapecio
- Paralelogramo
- Polígono Regular
- Círculo
- Problemas y ejercicios
- TEOREMA FUNDAMENTAL DE CALCULO
El teorema fundamental del cálculo consiste (intuitivamente) en la afirmación de que la derivación e integración de una función son operaciones inversas. Esto significa que toda función continua integrable verifica que la derivada de su integral es igual a ella misma. Este teorema es central en la rama de las matemáticasdenominada análisis matemático o cálculo.El teorema es fundamental porque hasta entonces el cálculo aproximado de áreas -integrales- en el que se venía trabajando desde Arquímedes, era una rama de las matemáticas que se seguía por separado al cálculo diferencial que se venía desarrollando por Isaac Newton, Isaac Barrow y Gottfried Leibniz en el siglo XVIII y dio lugar a conceptos como el de las derivadas. Las integrales eran investigadas como formas de estudiar áreas y volúmenes, hasta que en ese punto de la historia ambas ramas convergieron, al demostrarse que el estudio del "área bajo una función" estaba íntimamente vinculado al cálculo diferencial, resultando la integración, la operación inversa a la derivación.Una consecuencia directa de este teorema es la regla de Barrow, denominada en ocasiones segundo teorema fundamental del cálculo, y que permite calcular la integral de una función utilizando la integral indefinida de la función al ser integrada.
- PARA LA FINALIZAR MI BLOG CONTINUACIÓN LES MUESTRO UN VÍDEO DE COMO RESOLVER UNA INTEGRAL



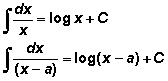
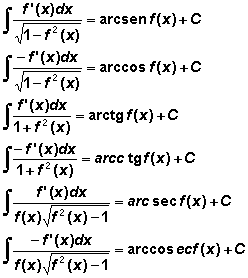
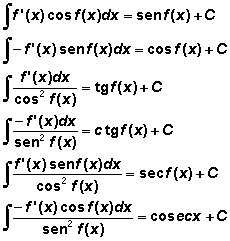
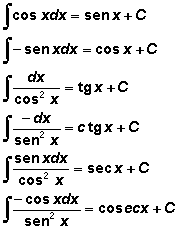








Violeta Garduño Zepeda
ResponderBorrarfalta informacion pero se que puedes hacerlo
Javier Armando Sarabia García
ResponderBorrarFaltan los videos e información
Luisa Angela García López
ResponderBorrarVas bien pero te falta bastante suerte
Nanci Karina Pérez Salgado
ResponderBorrarTe falta mucho pero sé que puedes hacerlo
JOSELYNE ESQUIVEL CARMONA: TE FALTA INFORMACIÓN, PERO VAS BIEN.... SIGUE ADELANTE....
ResponderBorrarSalvador Mariano Segundo compañera aunque te falta la información del temario tu puedes terminarlo
ResponderBorrartodavía te falta información suerte
ResponderBorrarDIANA LAURA PIÑA CRUZ
ResponderBorrarTE FALTA MUCHA INFORMACION PERO HECHALE GANAS TU PUEDES
MARIA HORTENSIA MUNGUIA ROMERO
VAS BIEN SE QUE TU PUEDES LOGRARLO EN VERDAD MUCHA SUERTE NIÑA
GERARDO PANIAGUA
ResponderBorrarbien compañera nada mas te falta complementar con informacion pero tu puedes
JORGE BULMARO PANIAGUA SANCHEZ
suerte compañera si se puede
JOSE ISRAEL HERNANDEZ PARADA
tu puedes compañera todo bien
te falta la información del temario, los ejercicios resueltos, el formulario, tu vídeo y tu foto de portada, suerte..
ResponderBorrarmaricruz medina reyes. orale compañera si k t ace falta muchisimo asi k exale ganitas te ace falta mas informacion,tu foto,ejercisios de la libreta,tu video suerte
ResponderBorrarhay bas echale ganas pero si te falta un poco mas
ResponderBorrarJose Antonio Vanegas Martinez; mmmmm te falta y te falto muchisimo compañera
ResponderBorrarTe falto muchísima información, ya no le aumentaste nada y el video donde esta
ResponderBorrar